澳门银河赌场注册送38-澳门银河赌场招人好招吗_百家乐德州_全讯网下载 (中国)·官方网站

中文題目：基于近似最小一乘的Hammerstein-Winner 時滯模型辨識

論文題目：Identification of Hammerstein-Wiener time delay model based on approximate least absolute deviation

錄用期刊/會議：International Journal of Modelling, Identification and Control (EI)

錄用/見刊時間：2022年06月

作者列表：

1） 徐寶昌 中國石油大學（北京）信息科學與工程學院/人工智能學院 自動化系教師

2） 榮志超 中國石油大學（北京）信息科學與工程學院/人工智能學院 碩18

3） 王雅欣 中國石油大學（北京）信息科學與工程學院/人工智能學院 博19

4） 袁力坤 中國石油大學（北京）信息科學與工程學院/人工智能學院 博17

文章簡介:

日益復雜的實際生產過程中存在著大量非線性過程。Hammerstein-Wiener模型是一種典型的塊連接模型，這種模型通過組合輸入非線性模塊、線性模塊、輸出非線性模塊來近似描述實際生產過程。同時，很多情況下存在不符合正態分布的尖峰噪聲和不確定的時滯。為了準確辨識出模型參數和時滯參數，提出了一種基于最小一乘準則函數的兩步辨識算法。

設計與實現:

圖1 Hammerstein-Wiener時滯模型結構圖

同時進行時滯參數和模型參數的辨識是比較困難的，因此將時滯參數和模型參數分開進行估計，提出了基于近似最小一乘準則函數的兩步法。這種方法的核心思想是模型參數和時滯參數分離開，進行交替估計。首先給定時滯參數一個初值，進行模型參數估計，然后根據模型參數估計時滯參數，直至模型參數和時滯參數都收斂至真值。仿真實驗表明，目標函數采用最小一乘準則的兩步法能夠有效抵抗尖峰噪聲的干擾，并且能夠準確估計出模型參數和時滯參數；基于最小二乘的辨識算法受到尖峰噪聲影響較大，甚至無法進行辨識。

實驗結果:

pH中和系統如圖2所示，代表容器容積，其中濃度為0.02mol/L的醋酸作為輸入流在連續攪拌釜反應器中通過濃度為0.5mol/L氫氧化鈉的滴定流進行滴定。滴定流分為和兩部分，為恒定的，由計算機信號進行調節。該pH中和過程可近似建模為Hammerstein-Wiener模型。

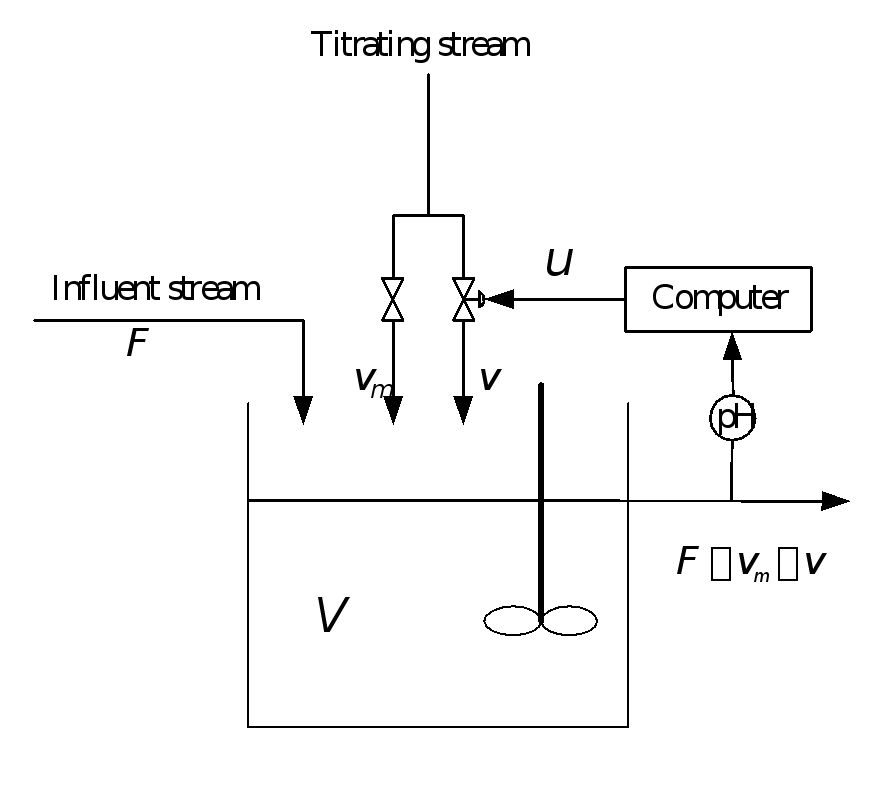
圖2 pH中和過程流程圖

當辨識過程中僅存在白噪聲時，基于最小一乘準則函數的兩步法（ALADSG）和基于最小二乘準則函數的兩步法（LSSG）的辨識曲線和辨識結果如圖3和表1所示。

圖3 僅含白噪聲時辨識曲線

表1 僅含白噪聲時辨識結果

觀察表1，可以看出兩種算法都可以估計出模型參數和時滯參數，觀察圖3，可以看出基于最小二乘的兩步法的相對誤差曲線能夠更快收斂，時滯參數能夠更早的穩定。因此，當辨識過程中僅存在白噪聲時，采用基于最小二乘的兩步法效率更高，符合以往的研究。

當辨識過程中存在概率為5%，幅值為白噪聲序列5倍的尖峰序列噪聲時，兩種算法的辨識曲線和辨識結果如圖4和表2所示。

圖4 =5%，A=5時辨識曲線

表2 =5%，A=5時辨識結果

根據表2可知，加入概率為5%，幅值為白噪聲序列5倍的尖峰序列噪聲后，最小二乘兩步法受到影響更大，辨識精度大幅下降；而最小一乘兩步法仍然能夠保持較高精度進行辨識。根據圖4可知，相比于僅含白噪聲，引入尖峰噪聲后，最小二乘兩步法相對誤差曲線波動變大，而最小一乘兩步法基本沒有變化。因此，當加入尖峰噪聲后，采用最小一乘兩步法辨識Hammerstein-Wiener模型優于最小二乘兩步法。

為了進一步驗證算法的魯棒性，加入概率為10%，幅值為白噪聲序列10倍的尖峰序列噪聲。兩種算法的辨識曲線和辨識結果如圖5和表3所示。

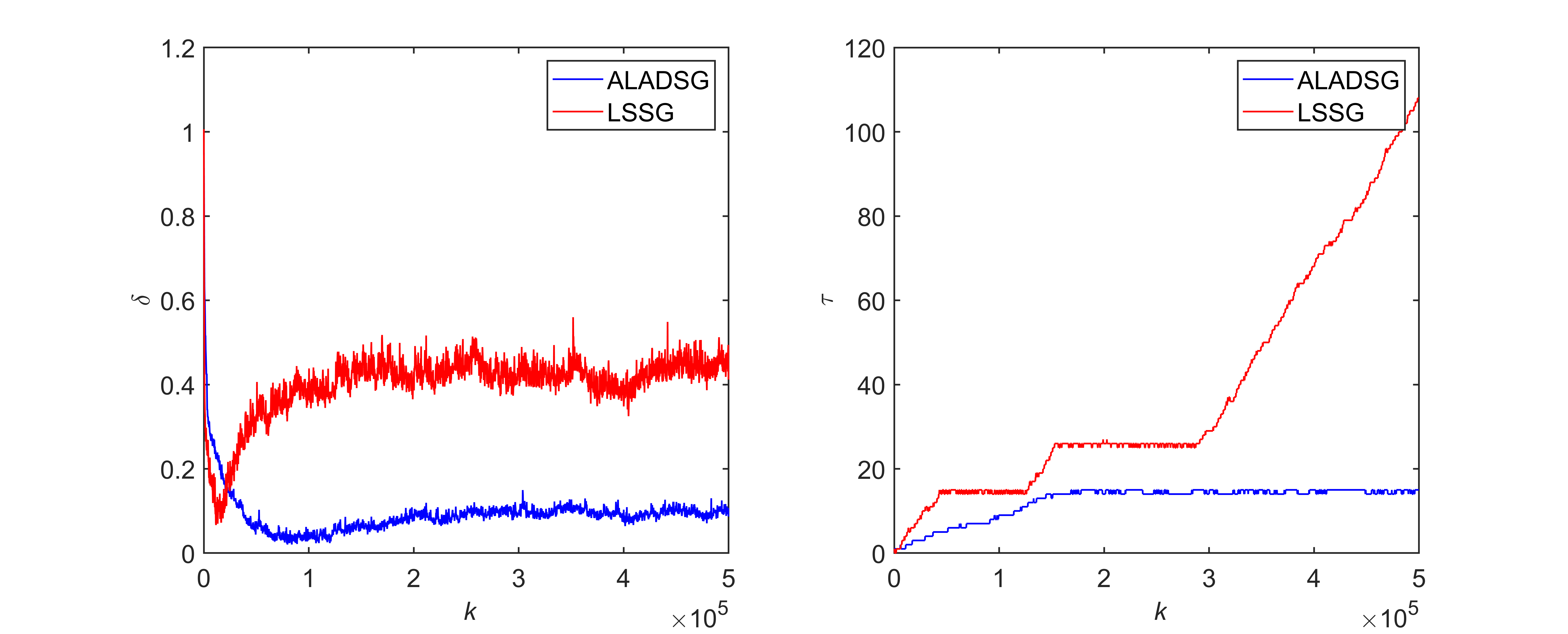
圖5 =10%，A=10時辨識曲線

表3 =10%，A=10時辨識結果

觀察表3和圖5可知，加入概率為10%，幅值為白噪聲序列10倍的尖峰序列噪聲后，最小二乘兩步法已經不能準確辨識模型參數，并且時滯參數也不能進行估計；最小一乘兩步法仍能較為準確的辨識模型參數，并且能夠準確估計出時滯參數，進一步驗證了最小一乘兩步法的魯棒性。

作者簡介:

徐寶昌，副教授，博士生導師，長期從事復雜系統的建模與先進控制；鉆井過程自動控制技術；井下信號的測量與處理；多傳感器信息融合與軟測量技術等方面的研究工作。現為中國石油學會會員，中國化工學會信息技術應用專業委員會委員。曾參與多項國家級、省部級科研課題的科研工作，并在國內外核心刊物發表了論文60余篇；其中被SCI、EI、ISTP收錄20余篇。