科研動(dòng)態(tài)
基于LMI的混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化解的狀態(tài)反饋實(shí)現(xiàn)方法：以催化裂化裝置為例
中文題目：基于LMI的混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化解的狀態(tài)反饋實(shí)現(xiàn)方法：以催化裂化裝置為例
論文題目：基于LMI的混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化解的狀態(tài)反饋實(shí)現(xiàn)方法：以催化裂化裝置為例
錄用期刊/會(huì)議：中國(guó)過程控制會(huì)議（CAA A類會(huì)議）
作者列表：
1） 汪曉蘇 中國(guó)石油大學(xué)（北京）人工智能學(xué)院 控制科學(xué)與工程 研22
2） 林嘉獎(jiǎng) 中國(guó)石油大學(xué)（北京）人工智能學(xué)院 自動(dòng)化系 教師
3） 羅雄麟 中國(guó)石油大學(xué)（北京）人工智能學(xué)院 自動(dòng)化系 教師
3） 許 鋒 中國(guó)石油大學(xué)（北京）人工智能學(xué)院 自動(dòng)化系 教師
摘要:
混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化問題的間歇操作解常直接應(yīng)用，然后再對(duì)連續(xù)操作解閉環(huán)化，這樣難以體現(xiàn)間歇操作對(duì)閉環(huán)控制的影響。本文先線性化混雜系統(tǒng)，再將動(dòng)態(tài)優(yōu)化閉環(huán)問題轉(zhuǎn)為跟蹤問題，并設(shè)計(jì)基于LMI的迭代算法求解。最后以催化裂化裝置為例驗(yàn)證方法的可行性。
背景與動(dòng)機(jī):
針對(duì)混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化問題，傳統(tǒng)的解決方法是將間歇操作解直接應(yīng)用，然后在對(duì)連續(xù)操作解閉環(huán)化，但這種方法無(wú)法體現(xiàn)間歇操作對(duì)閉環(huán)控制系統(tǒng)性能的影響。為了解決這一問題，首先對(duì)混雜參數(shù)系統(tǒng)線性化，然后通過求解混雜線性二次型調(diào)節(jié)器問題，進(jìn)一步優(yōu)化間歇操作對(duì)控制系統(tǒng)性能的影響，以實(shí)現(xiàn)更精確的控制和經(jīng)濟(jì)效益最大化。
設(shè)計(jì)與實(shí)現(xiàn):
本文首先介紹了混雜參數(shù)系統(tǒng)的動(dòng)態(tài)優(yōu)化問題的形式以及解法。然后說明了如何得到混雜參數(shù)系統(tǒng)的HLQR問題，以及如何將動(dòng)態(tài)優(yōu)化開環(huán)最優(yōu)解的實(shí)現(xiàn)問題轉(zhuǎn)化為HLQR問題，最后給出了HLQR問題的迭代LMI形式的解法。最后，以帶CO助燃劑的催化裂化裝置為例，說明了如何將本文的算法用到實(shí)際的工程問題中。
（1）混雜參數(shù)系統(tǒng)的動(dòng)態(tài)優(yōu)化問題
混雜參數(shù)系統(tǒng)指同時(shí)包含連續(xù)操作和間歇操作的系統(tǒng)。在數(shù)學(xué)上可以直接將間歇操作建模為微分、代數(shù)方程的參數(shù)，具體可以寫為：
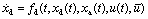
（2）線性混雜參數(shù)系統(tǒng)的HLQR問題
線性混雜參數(shù)系統(tǒng)是一種最簡(jiǎn)單的混雜參數(shù)系統(tǒng)，其中間歇操作在系統(tǒng)模型中以“線性”形式存在，具體可寫為：
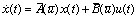
與LQR問題類似，HLQR問題的目標(biāo)函數(shù)也包含關(guān)于和的二次函數(shù)的積分項(xiàng)。由于HLQR問題多了間歇操作，因此HLQR問題的目標(biāo)函數(shù)還需要添加一項(xiàng)關(guān)于的二次項(xiàng)，即
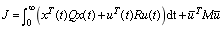
（3）動(dòng)態(tài)優(yōu)化問題最優(yōu)解的閉環(huán)實(shí)現(xiàn)
通過將動(dòng)態(tài)優(yōu)化問題的開環(huán)最優(yōu)解當(dāng)成目標(biāo)軌跡，可以將混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化問題最優(yōu)解的閉環(huán)實(shí)現(xiàn)轉(zhuǎn)化為HLQR問題，此時(shí)可以進(jìn)一步考慮間歇操作對(duì)系統(tǒng)控制性能的影響。
（4）HLQR問題的LMI解法
LQR問題的LMI形式可以由其對(duì)應(yīng)的H2控制問題得到。與之類似，可以得到HLQR問題的BMI形式,在經(jīng)過兩次Finsler’s引理松弛后得到：
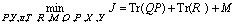
s.t.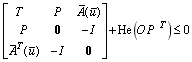
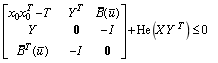
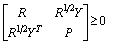
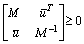
下面給出了具體的算法流程。
實(shí)驗(yàn)結(jié)果及分析:
針對(duì)催化裂化裝置，對(duì)其線性化和降階后，將動(dòng)態(tài)優(yōu)化的連續(xù)操作變量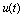
選為反應(yīng)溫度的設(shè)定值
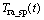和主風(fēng)流量
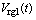，間歇操作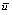
選為CO助燃劑的添加量
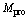。下面給出了算法的迭代過程和實(shí)驗(yàn)結(jié)果。
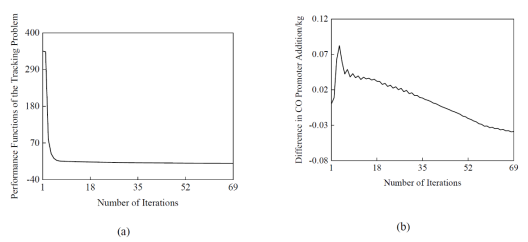
圖1 算法1的迭代過程：(a)跟蹤問題的性能函數(shù)；(b)CO助燃劑的差值
圖3 干擾下的開環(huán)解狀態(tài)反饋實(shí)現(xiàn)：(a)提升管反應(yīng)溫度；(b)主風(fēng)流量；(c)稀相段溫升；(d)煙氣氧氣含量
結(jié)論:
本文探討了混雜參數(shù)系統(tǒng)動(dòng)態(tài)優(yōu)化問題中開環(huán)最優(yōu)解的閉環(huán)實(shí)現(xiàn)。這通常指連續(xù)操作最優(yōu)解的閉環(huán)實(shí)現(xiàn)，而間歇操作最優(yōu)解則直接應(yīng)用。在化工系統(tǒng)中，動(dòng)態(tài)優(yōu)化目標(biāo)多為經(jīng)濟(jì)指標(biāo)，常獨(dú)立實(shí)現(xiàn)間歇與連續(xù)操作，卻忽視了間歇操作對(duì)系統(tǒng)控制性能的影響。因此，最佳方法是在設(shè)計(jì)控制系統(tǒng)時(shí)納入間歇操作的影響。本文先線性化混雜參數(shù)系統(tǒng)，再將閉環(huán)實(shí)現(xiàn)問題轉(zhuǎn)化為HLQR問題，即BMI問題，需迭代算法轉(zhuǎn)為L(zhǎng)MI問題求解，保證目標(biāo)函數(shù)單調(diào)不增。以催化裂化裝置為例，說明HLQR構(gòu)造方法。計(jì)算結(jié)果顯示，CO助燃劑添加量增多會(huì)加劇系統(tǒng)動(dòng)態(tài)變化，不利于控制，故間歇操作實(shí)現(xiàn)應(yīng)略小于最優(yōu)解。
通訊作者簡(jiǎn)介:
林嘉獎(jiǎng)于2020年畢業(yè)于中國(guó)石油大學(xué)（北京）獲控制科學(xué)與工程博士學(xué)位。目前就職于中國(guó)石油大學(xué)（北京）自動(dòng)化系，助理教授。主要研究方向包括魯棒控制，自適應(yīng)動(dòng)態(tài)規(guī)劃，最優(yōu)控制，混雜參數(shù)系統(tǒng)及其在化工過程等中的應(yīng)用。