MSH：一種用于非線性直流仿真的高阻節點感知的多階段同倫方法
中文題目：MSH：一種用于非線性直流仿真的高阻節點感知的多階段同倫方法
論文題目：MSH: A Multi-Stage HiZ-Aware Homotopy Framework for Nonlinear DC Analysis
錄用期刊/會議：2024 Design, Automation and Test in Europe Conference (DATE) (CCF-B類會議)
原文鏈接：https://ieeexplore.ieee.org/document/10546783
錄用/見刊時間：2024-3-25
作者列表：
1）金 洲 中國石油大學（北京）人工智能學院 計算機系教師
2）馮 田 成都華大九天科技有限公司
3）吳 梟 北京華大九天科技股份有限公司
4）牛 丹 東南大學 自動化學院
5）周振亞 北京華大九天科技股份有限公司
6）卓 成 浙江大學 信息科學與電子工程學院
背景與動機:
非線性直流分析是晶體管級電路仿真中最重要的任務之一。同倫法在改善牛頓-拉夫遜（NR）方法的收斂性問題方面取得了巨大成功。然而，在某些高阻（HiZ）節點處嵌入同倫參數可能會導致該類節點在同倫參數達到1時的節點電壓遠離真實的直流解，即使理論上此刻的電路應該等價于原始電路，從而導致在最終的NR驗證階段出現新的收斂失敗問題。在本文中，我們提出了一種HiZ節點感知的多階段同倫框架MSH，使HiZ節點和其他節點能夠分別進行多階段延拓，以增強仿真的收斂性。
設計與實現:
（1）特定 HiZ 節點引起的 DC 收斂失敗現象
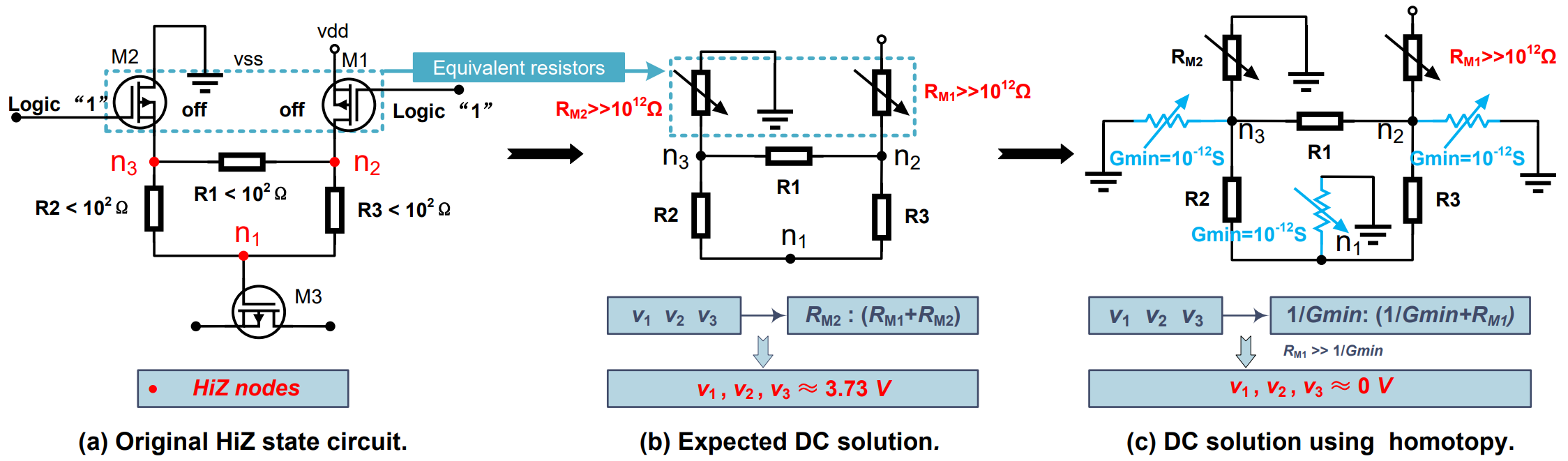
圖1：同倫算法中由特定 HiZ 節點引起的 DC 收斂失敗示意圖
如圖所示，當節點 n1~n3 呈高阻態時，晶體管M1和M2可以等效為兩個無窮大的電阻。此時，節點 n1~n3的電壓由RM2 與（RM1+RM2）的比值所決定，如圖1（b），在該電路中，經計算可以得到 v1 = v2 = v3 ≈ 3.73 V。當使用同倫法對上述電路進行求解時，如圖1（c）所示，節點 n1~n3的電壓由1/Gmin與（1/Gmin+RM1）的比值所決定，由于 RM1（>>1e12 Ω）通常遠遠大于 1/Gmin（≈1e12 Ω），所以此刻有 v1 = v2 = v3 ≈ 0 V，這將會導致最終 NR 驗證的失敗。
（2）多階段同倫框架
l多階段-多參數同倫框架
該框架的同倫函數如下：
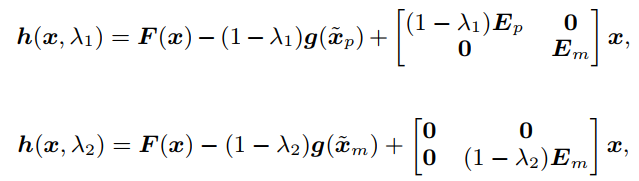
其中，
為第一階段的延拓方程，主要求解所有HiZ節點使其達到穩定狀態。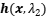
為第二階段的延拓方程，主要求解所有非HiZ節點。
lMOS可變增益同倫方程
為了進一步提升所提出的多參數-兩階段同倫算法在仿真MOS 電路時的效率，本文提出了一種 MOS 電流增益同倫方程（MCGH），以使得其解曲線更加平滑，從而實現快速 DC 仿真。如下公式所示，我們給MOS晶體管的漏源電流ids乘以了同倫參數λ，λ從0~1逐漸變化，以實現增益電流的連續變化。
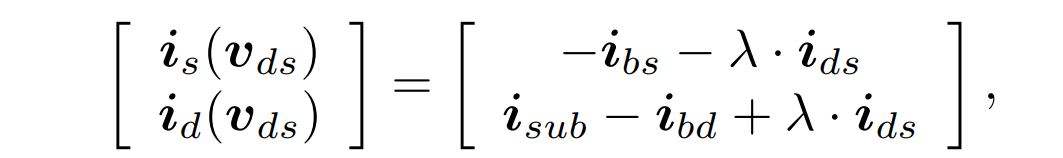
l弧長法追蹤解曲線
同時，為了更好地保證收斂性，我們采取了弧長法對同倫方程的解曲線進行追蹤。該方法主要分為預測和校正兩個階段。其預測階段的需要求解的方程如下：
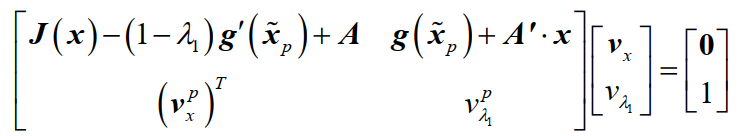
校正階段的需要求解的方程如下：
（3）HiZ節點的定位
本研究引入了一種簡單而有效的技術來識別這類具有 DC 路徑的 HiZ 節點。首先使用普通的 DC 算法對電路進行 DC 仿真。如果當右端項 RHS 足夠接近 0 時出現了不收斂情況，首先檢查每個不收斂節點的電流。如果節點電流小于給定閾值，則將該節點標記為 HiZ 節點。這樣，該算法就可以在不引入額外開銷的情況下，精確地定位具有 DC 路徑的 HiZ 節點。
實驗結果及分析:
（1）消除HiZ不收斂問題的有效性
圖2：(a)兩種方法下HiZ節點的解曲線；(b) λ2非常接近1時的局部放大圖
本文對一個工業 CMOS 電路進行了測試，該電路由 69334 個器件（包括 715 個 MOS 晶體管）組成，其具有16個HiZ節點。由圖可知，SOTA同倫可以成功收斂，但在最終NR驗證階段不能收斂。MSH框架收斂成功。
（2）MOS可變增益同倫的收斂性
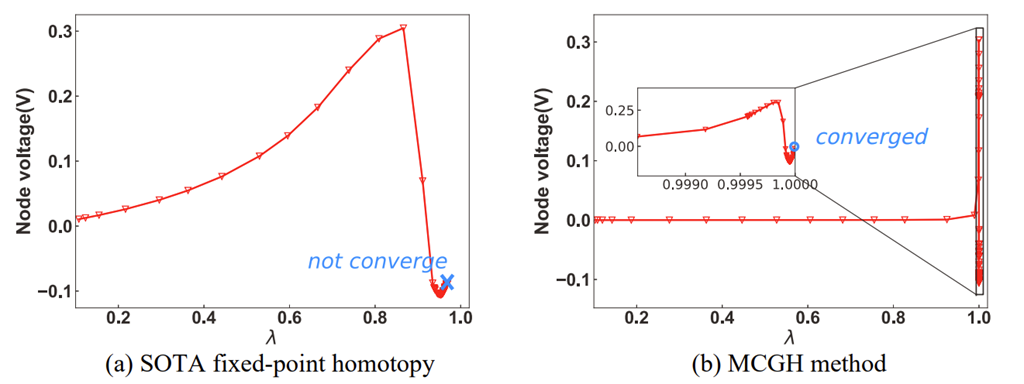
圖3：兩種同倫方法下MOSFET漏極節點的解曲線
由圖可知，對于SOTA同倫，由于電流增益的強非線性，當λ達到0.96左右時，解曲線出現不連續。而本文所提出的MCGH可以收斂，并且λ最終迭代到1。此外，可以發現當λ在0~0.999之間時，我們方法的解曲線非常光滑，λ = 1附近的波動主要是由于我們引入的線性輔助算子所導致的。
（3）加速效率
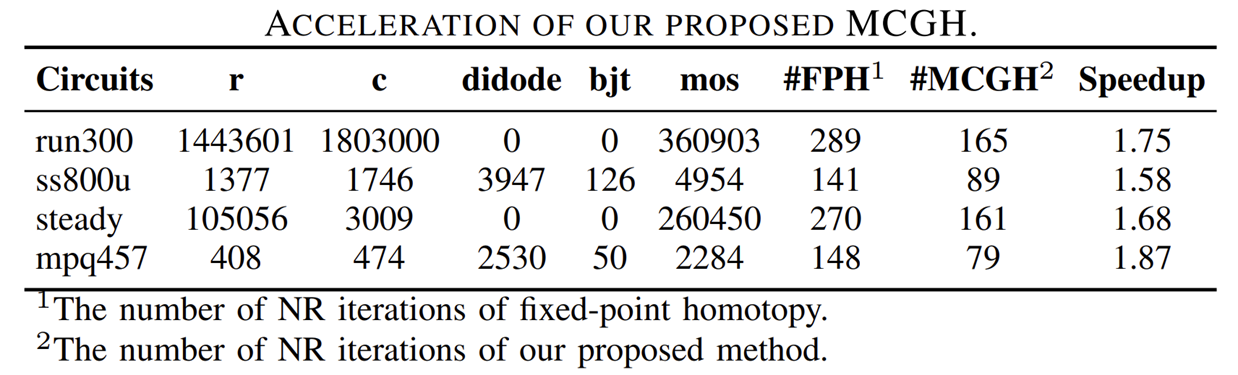
最后，基于本文所提出的 MSH 框架帶來的收斂性提升，我們進一步評估了MCGH函數相比于SOTA同倫函數的加速效率。結果顯示，基于MCGH函數的多階段同倫框架相較于基于SOTA同倫函數的多階段同倫框架大約平均加速了1.7倍。
結論:
本文提出了一種多參數同倫框架，可實現多階段延拓，以解決非線性直流分析中特定HiZ節點引起的DC收斂失敗問題。該框架采用全新的同倫函數實現快速延拓，采用弧長法對解曲線進行跟蹤，保證了其收斂性。本文通過工業界大規模電路證明了我們框架的有效性，并且該框架相較于比SOTA不動點同倫實現了1.7倍的平均加速比。
通訊作者簡介:
金洲，中國石油大學（北京）計算機系副教授，入選北京市科協青年人才托舉工程、校青年拔尖人才。主要從事集成電路設計自動化（EDA）、面向科學計算的DSA軟硬件協同設計等方面的研究工作。主持并參與國家自然科學基金青年項目、重點項目，科技部重點研發微納電子專項、高性能計算專項青年科學家項目，國家重點實驗室開放課題、企業橫向課題等。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要國際會議和期刊上發表60余篇高水平學術論文。獲EDA2青年科技獎、SC23最佳論文獎、ISEDA23榮譽論文獎、IEEJ九州支部長獎等。
聯系方式：jinzhou@cup.edu.cn