科研動(dòng)態(tài)
面向邊緣計(jì)算推薦系統(tǒng)的聯(lián)邦學(xué)習(xí)激勵(lì)機(jī)制設(shè)計(jì)
中文題目:面向邊緣計(jì)算推薦系統(tǒng)的聯(lián)邦學(xué)習(xí)激勵(lì)機(jī)制設(shè)計(jì)
論文題目:Incentive Mechanism Design of Federated Learning for Recommendation Systems in MEC
錄用期刊/會(huì)議:IEEE Transactions on Consumer Electronics (中科院大類2區(qū),JCR Q2)
原文DOI:10.1109/TCE.2023.3342187
原文鏈接:https://ieeexplore.ieee.org/abstract/document/10356897
錄用/見刊時(shí)間:2023-12-13
作者列表:
1)黃霽崴 中國石油大學(xué)(北京)信息科學(xué)與工程學(xué)院/人工智能學(xué)院 教授
2)馬博聞 中國石油大學(xué)(北京)信息科學(xué)與工程學(xué)院/人工智能學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)專業(yè) 碩21
3)王 名 中國聯(lián)通 工程師
4)Xiaokang Zhou Shiga University Faculty of Data Science Associate Professor
5)Lina Yao CSIRO's Data61 Senior Principal Research Scientist
6)Shoujin Wang University of Technology Sydney Data Science Institute Lecturer
7)齊連永 中國石油大學(xué)(華東)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院 教授
8)陳 瑩 北京信息科技大學(xué) 計(jì)算機(jī)學(xué)院 教授
摘要:
隨著消費(fèi)電子產(chǎn)品和通信技術(shù)的快速發(fā)展,網(wǎng)絡(luò)邊緣的終端用戶產(chǎn)生了大量數(shù)據(jù),現(xiàn)代推薦系統(tǒng)充分利用這些數(shù)據(jù)來訓(xùn)練各種人工智模型。然而,傳統(tǒng)的集中式模型訓(xùn)練必須將所有數(shù)據(jù)傳輸?shù)皆贫朔?wù)器,存在隱私泄露和資源短缺的問題。因此,移動(dòng)邊緣計(jì)算(MEC)與聯(lián)邦學(xué)習(xí)相結(jié)合被認(rèn)為是解決這些問題的一種有前途的模式。智能設(shè)備可以為聯(lián)邦學(xué)習(xí)提供數(shù)據(jù)和計(jì)算資源,并將本地模型參數(shù)傳輸?shù)脚鋫溥吘壏?wù)器的基站,以聚合成一個(gè)全局模型。然而,由于物理資源有限和隱私泄露的風(fēng)險(xiǎn),用戶并不愿意自愿參與聯(lián)邦學(xué)習(xí)。為解決這一問題,本文利用博弈論提出了一種基于兩階段Stackelberg博弈的激勵(lì)機(jī)制,以激勵(lì)用戶為聯(lián)邦學(xué)習(xí)貢獻(xiàn)計(jì)算資源。本文為用戶和基站定義了兩個(gè)效用函數(shù),并提出了效用最大化問題。通過理論分析,得到了用戶的納什均衡策略和效用最大化問題的Stackelberg均衡。此外,本文還提出了一種基于博弈的激勵(lì)機(jī)制算法(GIMA)來實(shí)現(xiàn)Stackelberg均衡。最后,本文提供了仿真結(jié)果來驗(yàn)證GIMA算法的性能。實(shí)驗(yàn)結(jié)果表明,與其他激勵(lì)方法相比,本文提出的算法收斂速度快,能獲得更高的效用值。
背景與動(dòng)機(jī):
在本文中,為了激勵(lì)用戶貢獻(xiàn)更多計(jì)算資源以提高聯(lián)邦學(xué)習(xí)模型的性能,本文利用博弈論將基站和用戶之間的聯(lián)邦學(xué)習(xí)培訓(xùn)建模為一個(gè)兩階段的Stackelberg博弈,其中基站是領(lǐng)導(dǎo)者,用戶是追隨者。配備服務(wù)器的基站發(fā)起聯(lián)邦學(xué)習(xí)任務(wù)并支付費(fèi)用。基站覆蓋范圍內(nèi)的用戶通過貢獻(xiàn)計(jì)算資源和本地?cái)?shù)據(jù)樣本參與聯(lián)邦學(xué)習(xí)。基站和用戶的目標(biāo)是最大化各自的效用。本文從理論上分析了效用最大化問題的Stackelberg均衡的存在性,并提出了一種基于博弈的激勵(lì)機(jī)制算法(GIMA)來解決用戶和基站的效用最大化問題。
主要內(nèi)容:
本文考慮蜂窩網(wǎng)絡(luò)環(huán)境下推薦系統(tǒng)的典型聯(lián)邦學(xué)習(xí)場景,如圖1所示。它由一個(gè)帶有邊緣服務(wù)器的基站和多個(gè)用戶組成。每個(gè)用戶使用本地原始數(shù)據(jù)訓(xùn)練自己的本地推薦模型。然后,只將局部模型的參數(shù)上傳到邊緣服務(wù)器進(jìn)行聚合,即可獲得全局模型。最后,聚合的全局模型被發(fā)送回用戶設(shè)備進(jìn)行推理和下一次迭代訓(xùn)練。

圖1 MEC中推薦系統(tǒng)的聯(lián)邦學(xué)習(xí)系統(tǒng)模型
本文定義了基站和用戶的效用函數(shù),隨后提出兩階段Stackelberg博弈框架來捕獲參與聯(lián)邦學(xué)習(xí)的各方之間的復(fù)雜互動(dòng)。基站需要決定一個(gè)適當(dāng)?shù)募?lì)方式來吸引用戶參與,以獲得高質(zhì)量的模型。用戶需要決定他們的參與程度,以最大化他們的效用。因此,優(yōu)化問題可表示為
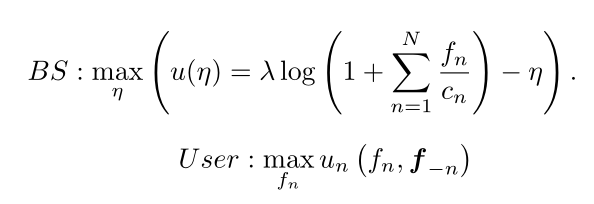
隨后證明了納什均衡的存在性以及Stackelberg均衡的存在,并且提出了一種基于博弈的激勵(lì)機(jī)制算法(GIMA)來實(shí)現(xiàn)Stackelberg均衡,算法偽代碼如下所示:

實(shí)驗(yàn)結(jié)果及分析:
從圖2可以看出,基站和用戶存在唯一的Stackelberg均衡策略。為了驗(yàn)證唯一Stackelberg均衡的存在性,在用戶數(shù)量和用戶策略固定的情況下,將支付從0變化到50。基站的效用曲線呈凸形,曲線最高點(diǎn)為Stackelberg均衡的最佳響應(yīng)。本文還驗(yàn)證了用戶間的唯一納什均衡,對(duì)于每個(gè)用戶根據(jù)其他用戶和基站支付的固定策略改變頻率。值得注意的是,每個(gè)用戶的效用曲線都是凸的。在這種情況下,用戶可以通過確定計(jì)算資源的策略來最大化效用。
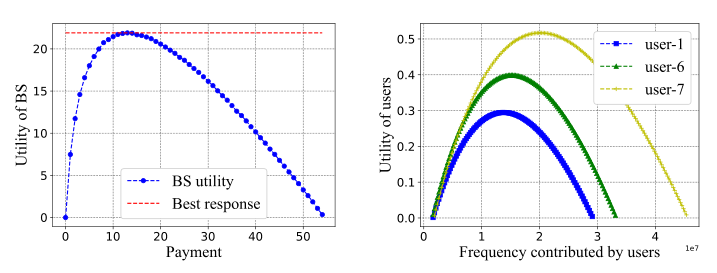
圖2 納什均衡及Stackelberg均衡
圖3顯示了基站和用戶的效用變化情,展示了不同用戶數(shù)下Random算法、GIMA算法和Fix算法效用。本文提出的的GIMA算法的基站效用是三種算法中最大的。隨著用戶數(shù)量的增加,GIMA算法與其他兩種算法之間的效用差距越來越大。此外,GIMA算法的增長速度比線性增長慢。實(shí)際上,隨著用戶數(shù)量的進(jìn)一步增加,越來越多的用戶參與到聯(lián)邦學(xué)習(xí)訓(xùn)練中,基站可以獲得大量的計(jì)算資源。但是,為了獲得最大的效用,基站所需的計(jì)算資源量會(huì)趨于穩(wěn)定。此外,隨著用戶數(shù)量的增加,用戶的平均效用減少。這是因?yàn)殡S著用戶數(shù)量的增加,參與聯(lián)邦學(xué)習(xí)訓(xùn)練的用戶越來越多,而獎(jiǎng)勵(lì)的增長速度卻持平。因此,用戶的平均效用變小。可以明顯看出,GIMA算法的基站效用是三種算法中最大的,GIMA算法與另外兩種算法的用戶平均效用差距越來越大。
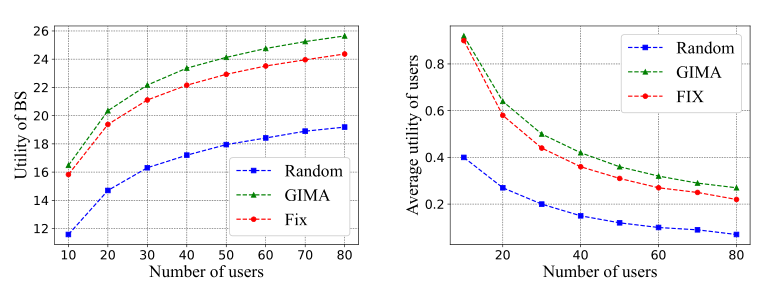
圖3 不同用戶數(shù)量下的基站效用及用戶平均效用
結(jié)論:
本文研究了一種與聯(lián)邦學(xué)習(xí)合作的MEC系統(tǒng),用于基站覆蓋范圍內(nèi)的推薦系統(tǒng)。基站有償發(fā)布聯(lián)邦學(xué)習(xí)任務(wù),用戶通過貢獻(xiàn)計(jì)算資源和本地?cái)?shù)據(jù)競爭獲利。本文為用戶和基站設(shè)計(jì)了兩個(gè)效用函數(shù),還將效用最大化問題表述為兩階段Stackelberg博弈,并從理論上證明了Stackelberg均衡的存在。然后,本文提出了GIMA算法,以在有限的迭代次數(shù)內(nèi)獲得用戶和基站的均衡策略。通過模擬實(shí)驗(yàn)說明,與其他激勵(lì)方法相比,GIMA算法能快速收斂并獲得更高的效用值。在今后的工作中,我們將考慮數(shù)據(jù)新鮮度的影響,鼓勵(lì)用戶提供新鮮數(shù)據(jù),以訓(xùn)練出更精確的模型。我們將進(jìn)一步考慮數(shù)據(jù)樣本不足的問題,并研究聯(lián)邦學(xué)習(xí)的自適應(yīng)激勵(lì)機(jī)制框架。此外,我們還將從經(jīng)濟(jì)學(xué)角度探索各種激勵(lì)機(jī)制設(shè)計(jì)方法,如反向拍賣等。
通訊作者簡介:
黃霽崴,教授,博士生導(dǎo)師,中國石油大學(xué)(北京)信息科學(xué)與工程學(xué)院/人工智能學(xué)院副院長,石油數(shù)據(jù)挖掘北京市重點(diǎn)實(shí)驗(yàn)室主任。入選北京市優(yōu)秀人才、北京市科技新星、北京市國家治理青年人才、昌聚工程青年人才、中國石油大學(xué)(北京)優(yōu)秀青年學(xué)者。本科和博士畢業(yè)于清華大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)系,美國佐治亞理工學(xué)院聯(lián)合培養(yǎng)博士生。研究方向包括:物聯(lián)網(wǎng)、服務(wù)計(jì)算、邊緣智能等。已主持國家自然科學(xué)基金、國家重點(diǎn)研發(fā)計(jì)劃、北京市自然科學(xué)基金等科研項(xiàng)目18項(xiàng);以第一/通訊作者在國內(nèi)外著名期刊和會(huì)議發(fā)表學(xué)術(shù)論文60余篇,其中1篇獲得中國科協(xié)優(yōu)秀論文獎(jiǎng),2篇入選ESI熱點(diǎn)論文,4篇入選ESI高被引論文;出版學(xué)術(shù)專著1部;獲得國家發(fā)明專利6項(xiàng)、軟件著作權(quán)4項(xiàng);獲得中國通信學(xué)會(huì)科學(xué)技術(shù)一等獎(jiǎng)1項(xiàng)、中國產(chǎn)學(xué)研合作創(chuàng)新成果一等獎(jiǎng)1項(xiàng)、廣東省計(jì)算機(jī)學(xué)會(huì)科學(xué)技術(shù)二等獎(jiǎng)1項(xiàng)。擔(dān)任中國計(jì)算機(jī)學(xué)會(huì)(CCF)服務(wù)計(jì)算專委會(huì)委員、秘書,CCF和IEEE高級(jí)會(huì)員,電子學(xué)報(bào)、Chinese Journal of Electronics、Scientific Programming等期刊編委。

