基于工程經驗的群智能通用PID參數整定
中文題目：基于工程經驗的群智能通用PID參數整定
論文題目：Engineering experience-based swarm intelligence for generalized PID tuning
錄用會議：2025 IEEE 14th Data Driven Control and Learning Systems Conference(CAA-A類會議)
錄用時間： 2025.03.20
作者列表：
1）王鎧銘 中國石油大學（北京）人工智能學院 控制科學與工程 碩23
2）王 珠 中國石油大學（北京）人工智能學院 自動化系教師
3）周建橋 中國石油大學（北京）人工智能學院 控制科學與工程 博21
摘要:
PID控制器被廣泛應用于工業過程控制中。然而，傳統PID參數整定方法在應用于復雜的動態系統時，尤其是在變工況條件下，往往會面臨很大的局限性。這些挑戰可能導致經驗不可行解(EIS)問題。為緩解這一問題，本文提出了一種將工程經驗與粒子群優化(PSO)相結合的PID調節方法。通過定義參數空間并引入參數物理優化方向約束，該方法有效避免了 EIS 的發生。通過數值模擬，基于工程經驗的Levy-Memory-PSO (EE-LMPSO)算法被用于優化PID參數。通過與傳統方法的比較，證明了該算法在優化性能、可靠性和控制精度方面的優勢。實驗結果表明，所提出的方法提高了調整效率，增強了系統穩定性，并在復雜的動態環境中實現了更好的控制性能。
背景與動機:
PID參數以實現精確穩定的閉環控制被認為是一個"NP-Hard"問題，類似于所有非凸優化問題。PSO具有全局搜索能力，且實施簡單，因此在PID參數優化方面越來越受歡迎。但在實際應用中，其優化結果可能在數學上滿足目標函數，但卻不符合工程預期，即EIS問題。造成EIS問題的主要原因是參數空間配置不合理、缺乏參數物理優化約束以及目標函數設計不當。
設計與實現:
1)開環增益內核準則(Rule.1)
通過帶有Nussbaum Gain的在線遞推辨識算法，構建系統的高階線性時變模型，得到時變參數后計算當前工況下的開環增益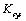
, 基于該增益，限定比例增益
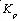的初始參數空間:
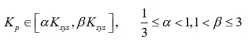
2)積分-微分時間比例準則(Rule.2)
針對不同系統延遲特性，引入積分與微分時間的比例因子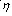
, 可根據延遲程度自適應調整動態響應，約束關系:
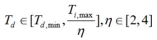
3)比例-積分優化協調準則(Rule.3)
當粒子群迭代收斂中后期，與
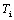同時偏離其最優解趨勢時，系統可能陷入局部最優或無效搜索。為此引入動態協調機制：當兩參數相對偏差超過設定閾值時，觸發粒子位置隨機重置。
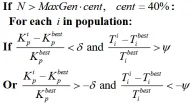
主要內容:
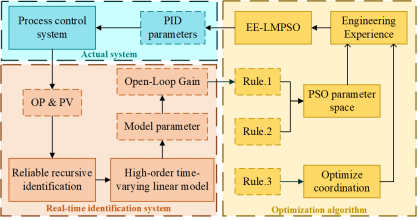
EE-LMPSO-PID在線閉環智能調整控制器參數的方案如下：
1) 數據采集：在當前的控制系統中，首先確定采樣頻率，然后采集控制回路的操縱變量(OP)和過程變量(PV);
2) 建立模型：使用高階線性時變模型捕捉對象的動態特性，并將模型開環增益賦予Rule.1;
3) 確定目標函數：根據綜合性能指標選擇合適的
和
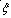值;
4) 初始化：根據規則Rule.1和Rule.2形成PSO初始化空間，并設置PSO超參數;
5) 計算適合度函數;
6) 更新粒子的速度和位置;
7) 更新全局最優位置;
8) 參數優化約束：引入Rule.3;
9) 重復步驟5)至8)，直至滿足終止條件;
10) 輸出PID最佳參數。
實驗結果及分析:
為了驗證將EE納入LMPSO的有效性，并評估其針對EIS的預防能力。本研究以數值仿真作為對象，通過對比實驗，揭示EE對LMPSO優化效率的提升及其降低EIS 發生概率的能力。實驗工作流程包括四項內容：
1)構建基于Rule.1和Rule.2形成的理論參數空間和經過多次實驗積累形成的經驗參數空間(ME-LMPSO)，并比較兩者在相同實驗條件下的優化性能。
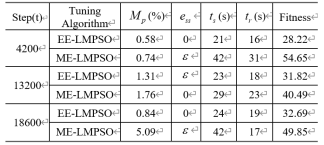
表 1 EE-LMPSO 和 ME-LMPSO 優化性能對比表
2)通過是否啟用Rule.3驗證粒子收斂速度和優化精度的性能差異，進而驗證其有效性。
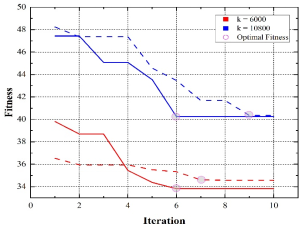
圖 1 比例-積分優化協調下的優化效率比較
3)在粒子數和迭代次數較少的條件下，通過多次獨立重復實驗，記錄并分析實驗中出現EIS的概率，從而比較有/無工程經驗的LMPSO在防止EIS問題上的能力差異。
表 2 EE-LMPSO和ME-LMPSO的EIS概率比較
4)通過比較和分析跟蹤精度、穩定性和響應時間的差異，評估輸出跟蹤參考輸入的可靠性。
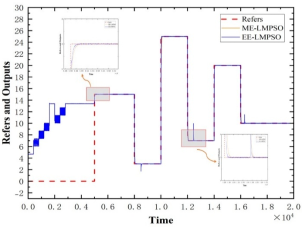
圖 2 ME-LMPSO和EE-LMPSO輸出跟蹤參考輸入
實驗結果綜合表明，所提出的 EE-LMPSO 方法在多個方面具有明顯優勢：其構建的參數空間更合理，提升了整定性能（實驗一）；引入方向性約束優化了收斂效率（實驗二）；在資源受限條件下顯著降低了經驗不可行解發生概率（實驗三）；并在動態控制中實現了更優的跟蹤精度與系統穩定性（實驗四）。以上結果充分驗證了將工程經驗融入優化過程的有效性與實用性。
結論:
本文介紹的改進優化算法將物理工程經驗與群智能優化相結合，有效地緩解了傳統參數調整方法中經常出現的經驗不可行解的問題。仿真結果表明，在復雜的動態系統中，該方法比傳統方法更具優勢，尤其是在縮短調整時間和提高控制精度方面。進一步的實驗證實了將物理工程經驗融入優化過程的有益影響，突出了該方法在工業控制系統中廣泛應用的潛力。
通訊作者簡介:
王珠，博士，中共黨員，現任中國石油大學（北京）副教授、碩士生導師。2016年至今在中國石油大學（北京）自動化系工作，現任中國自動化學會人工智能技術與工業應用專業委員會委員、中國化工學會信息技術應用專業委員會青年委員、北京人工智能學會理事。
在科研與社會服務方面，研究興趣為系統辨識與智能控制、煉化過程動態異常診斷與故障預警、大數據質量預測與綜合優化。近年來，主持重點流程工業企業的高級智能報警項目數項以及國家自然科學基金項目，已發表高水平學術論文30余篇。